GEOMETRIA ANALITYCZNA Bardzo proszę o pomoc: Boki AB i AC trójkąta ABC zawarte są odpowiednio w prostych o równaniach x + y − 7 = 0 i x = 0. Oblicz współrzędne wierzchołków B i C gdy środkiem boku BC jest punkt S=(2,2). Proszę o wytłumaczenie.

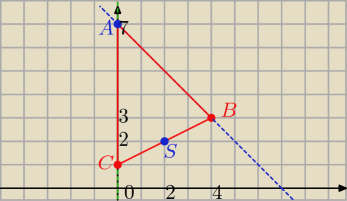
Eta: Proste AB i AC przecinają się w punkcie A ( 0,7) C( 0,y_c) bo należy do prostej AC: x= 0 B( x_B, − x_B+7) bo należy do prostej AC: y= −x +7 S(2,2) jes środkiem odcinka BC

	xC+xB		yC + yB
to: xS=		..... i yS=
	2		2

0+x_B= 4 ..... i y_C +y_B= 4 x_B= 4 to: B( 4, −4+7) => B( 4, 3) to: y_C= 4−y_B = 1 C( 0,1)